Long Memory Affine Aggregated ARCH process
(parameter set 1)

This process is build similarly to the LM-Aff-Mic-ARCH, but the historical volatilities are computed using aggregated returns. The time structure of the process is the same, with τk defined as a geometric series. The historical volatilities are defined by:

x(t) --x-(t---lkδt) r [lkδt](t) = √lk- (1) 2 2 2 σk(t) = μk σk(t - δt) + (1 - μk)r[lkδt] (t) i = 1,⋅⋅⋅,n.
The return at the time scale lkδt is the usual price difference, scaled from the time horizon lkδt to the time horizon δt using a random walk hypothesis. In this way, all returns r[lkδt] and volatilities σk are related to the same fundamental scale δt.

The effective volatility is defined as for the LM-Aff-Mic-ARCH model. This process has been introduced in Zumbach [2004].

The simulation uses a power law decay for the coefficients, with parameters:

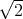
The innovations have a Student distribution with 3.3 degree of freedom. The simulation time corresponds to 200 years with a time increment δt = 3 minutes.

References

   Gilles Zumbach. Volatility processes and volatility forecast with long memory. Quantitative Finance, 4:70–86, 2004.