GARCH(1,1) with stochastic volatility mean

The mean volatility σ∞ and coupling constant w∞ are important parameters for all the affine ARCH processes, and the mechanism that sets their values is an interesting open question.

A possible explanation that the fundamental economic shifts induce price moves, and the term w∞σ∞² is a measure of the underlying economic activities and/or imbalances. In this explanation, the mean volatility level is set by long term economic fluctuations, with a dynamics given by a stochastic volatility process. Then, the dynamics of the financial markets is captured by an ARCH process.

The simplest process combining a long term exponential stochastic volatility with a short term GARCH(1,1) process is the following:

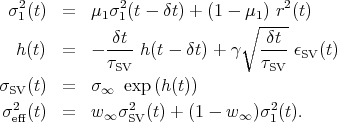
σ2(t) = μ1σ2 (t - δt) + (1 - μ1 ) r2(t) 1 1 ∘ ---- h(t) = - -δt-h(t - δt) + γ -δt-ϵ (t) τSV τSV SV σ (t) = σ exp (h(t)) S2V ∞ 2 2 σeff(t) = w ∞σ SV(t) + (1 - w ∞)σ1(t).

The characteristic time τ_SV fixes to the mean reversion time for the stochastic volatility.

The argument about the long term economic fluctuations would lead to τ_SV > τ_k.

The parameters have been chosen so as to visualize clearly the generic properties of a combined process. They are

σ∞ = 0.11.
w∞ = 0.5.
τ₁ = 0.33 day, equivalent to μ₁ = 0.99377 for the 3’ grid (for the GARCH(1,1) dynamics).
τ_SV = 14 day (for the stochastic volatility dynamics).
γ = 0.5.

The innovations have a Student distribution with 3.3 degree of freedom, while the innovations ϵ_SV for the stochastic volatility have a normal distribution. The simulation time corresponds to 200 years with a time increment δt = 3 minutes.