Long-Memory Affine Microscopic ARTCH (LM-Aff-Mic-ARTCH)

The similar process but without trend is the LM-Aff-Mic-ARCH process. The overall introduction for the processes with trend is given in the description for the GARTCH(1,1) process.

For the multi-component processes with trend, the historical volatilities σ_k are computed as without trend. The effective volatility is modified to add the effect of the past trends at the time horizons present in the process

km∑ax km∑ax σ2eff(t) = wk σ2k(t) + w∞ σ2∞ + θk r[lk](t) r[lk](t - lkδt) (1) k=1 k=1 ∑ wk = (1 - w ∞ )χk with χk = 1 (2) k

For a power law decay, the coefficients are set with

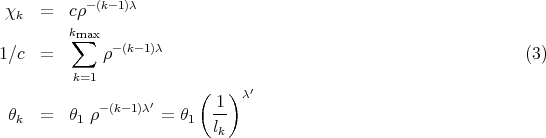
χk = cρ- (k-1)λ km∑ax 1 ∕c = ρ-(k- 1)λ (3) k=1 ( ) λ′ -(k-1)λ′ -1 θk = θ1 ρ = θ1 lk

The parameters for the simulations are

σ∞ = 0.11
w∞ = 0.093
τ₁ = 1h20 min
ρ =
ρ^n-1 = 1024 (i.e. n = 21)
λ = 0.16
θ₁ = 0.38
λ′ = 1.7
The cross term returns use the lags given by l_k = ρ^k-1.

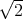
The innovations have a Student distribution with 3.3 degree of freedom. The simulation time corresponds to 200 years with a time increment δt = 3 minutes.