Heston process with normal innovations

The Heston model is a stochastic volatility process where the noise term for the variance dynamic is modulated by the volatility. The equations are:

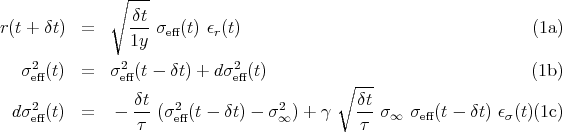
∘ --- r(t + δt) = δt-σeff(t) ϵr(t) (1a) 1y 2 2 2 σ eff(t) = σ eff(t - δt) + d σeff(t) ∘ --- (1b) 2 δt 2 2 δt dσ eff(t) = - -- (σeff(t - δt) - σ∞ ) + γ -- σ∞ σeff(t - δt) ϵσ(t)(1c) τ τ

where σeff²(t) is an annualized variance, σ ∞² fixes the mean annualized variance, τ sets the mean reversion time to the mean variance, and γ is the mean noise level. The main interest of the model is that an exact solution for the European option price can be computed when the residues ϵ_r and ϵ_σ are Gaussian, see Heston and Nandi [2000].

The parameters for the simulations are:

σ∞ = 0.11.
τ = 4 days.
γ = 1.65
p(ϵ_r), p(ϵ_σ): normal distributions.

The simulation time corresponds to 200 years with a time increment δt = 3 minutes.

References

S. Heston and S. Nandi. A closed-form GARCH option pricing model. Review of Financial Studies, 13:585–626, 2000.