Long Memory Heston process

The long memory Heston process is a minimal modification of the Heston process so as to introduce a volatility cascade. The equations for the model with n components are:

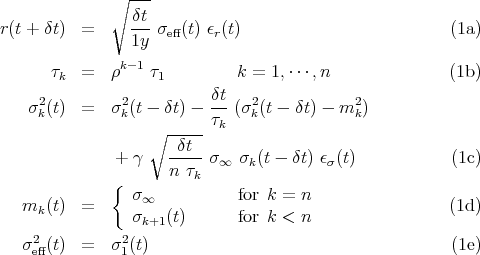
∘ --- r(t + δt) = δt- σeff (t) ϵr(t) (1a) 1y k-1 τk = ρ τ1 k = 1,⋅⋅⋅,n (1b) 2 2 δt 2 2 σ k(t) = σk(t - δt) - τk (σk(t - δt) - m k) ∘ ----- + γ -δt--σ∞ σk(t - δt) ϵσ(t) (1c) n τk { σ ∞ for k = n mk (t) = (1d) σk+1 (t) for k < n σ2eff(t) = σ21(t) (1e)

where all the volatilities σ∞, σeff(t) and σ_k(t) are annualized. The parameter σ∞ fixes the mean annualized volatility, the vector τ_k sets the mean reversion time for σ_k, and γ is the noise level for the volatility. The equations for the volatility are iterated starting from k = n and decreasing, so as to incorporate in the scale k the new information at the scale k + 1 at the time t.

The parameters for the simulations are:

σ∞ = 0.11.
τ₁ = 1/32 day.
τ_n = 32 day.
ρ = 2.
γ = 1.2
p(ϵ_r): Student with 4.0 degree of freedom
p(ϵ_σ): Student with 4.0 degree of freedom

The simulation time corresponds to 200 years with a time increment δt = 3 minutes.